Rouler en vélo, sur le plat, en côte, en descente, lutter contre le vent ou profiter d'un vent favorable, tout cela obéit à des lois de la physique et de la mécanique. Nous allons essayer de mettre cela en équation, de façon la plus simple possible. Peut être que certaines conclusions iront contre des idées reçues.

L'énergie.

Tout exercice physique demande une dépense d'énergie. Cette énergie s'exprime dans une unité que l'on appelle des joules. C'est une unité qui ne nous est pas beaucoup familière, sauf peut être pour les dames car, sur les emballages de friandises ou autres produits alimentaires, on peut voir l'énergie qu'ils contiennent exprimée en joules et son équivalent en calorie.

Gravissez un étage dans votre escalier, c'est à dire vous montez de 3 mètres. Vous pesez soixante quinze kilos, mais là encore il faut utiliser une unité non familière, le Newton, c'est l'unité internationale, c'est à cause de la mondialisation. Un Newton, c'est tout simplement 100 grammes. Donc vous pesez 750 Newtons. L'énergie dépensée, c'est la force qu'il faut vaincre pour monter multipliée par le déplacement vertical. La force à vaincre, c'est cette fichue pesanteur qui vous incite plutôt à prendre l'ascenseur et la force de pesanteur, c'est votre poids. Vous allez donc dépenser une énergie de  :      750 Newton x 3 m = 2250 joules

La puissance.

Est-ce fatigant de dépenser 2250 joules, autrement dit de gagner votre étage ? Tout dépend du temps que vous allez mettre, vous pouvez gravir les marches quatre à quatre ou prendre tout votre temps. C'est alors qu'intervient la notion de puissance.

La puissance, c'est l'énergie que vous allez dépenser par seconde. Elle s'exprime en watt. C'est une unité plus familière, on sait ce que représente une ampoule de 40 watts ou une ampoule de 100 watts, le bricoleur fait la différence entre une perceuse de 100 watts et de 500 watts.

La puissance, c'est donc l'énergie divisée par le temps exprimé en secondes. Si vous mettez 5 secondes pour gagner l'étage, vous avez développé une puissance de 2250 joules / 5 secondes = 450 watts, c'est très rapide, vous risquez un arrêt cardiaque, mettez plutôt 15 secondes, c'est plus raisonnable, vous développez alors 2250 joules /15 secondes = 150 watts.

Etant donné que l'énergie c'est une force multipliée par des mètres et que pour obtenir la puissance vous divisez par des secondes, on peut dire que la puissance c'est une force multipliée par une vitesse. Dans l'exemple précédent, la puissance, c'est 750 Newton x 0,20 m/s = 150 watts.

Donc:

puissance(en watt) = force à vaincre(en Newton) x vitesse(en m/s)

En vélo, quelle puissance développez-vous ? Il faut d'abord examiner les forces à vaincre.

Les forces à vaincre

Lorsque vous montez les escaliers, il faut vaincre la force de pesanteur qui vous attire irrémédiablement vers le bas: cette force, c'est votre poids.

En vélo, quelles forces faut-il vaincre ? Trois types de forces :

la force de pesanteur si vous gravissez une côte.

des forces de frottement entre les roues et la chaussée, cela dans tous les cas.

la force de résistance de l'air mais attention, ce qui compte, c'est le vent apparent. Il faut bien faire la distinction entre le vent apparent et le vent réel, les marins connaissent bien ça. Le vent apparent, c'est celui qui peut aussi bien vous caresser le visage que le cingler, il est fortement tributaire de la vitesse à laquelle vous roulez. Le vent réel, c'est celui que la météo vous donne, celui que vous ressentez uniquement lorsque vous êtes à l'arrêt.

A noter pour les puristes de la Mécanique: les forces que nous avons appelées "forces de frottement" sont en fait les forces denommées généralement "forces de résistance au roulement" dont les effets sont identiques à ceux de forces de frottement. Aussi, pour qu'il n'y ait pas de confusion entre forces de résistance au roulement et forces de résistance de l'air, nous avons préféré parler de "frottement".

Les forces de frottement.

Chacun a pu constater qu'il est plus facile de rouler sur une chaussée revêtue d'un bitume bien lisse que sur une route gravillonnée: le frottement n'est pas le même dans les deux cas.

La force de frottement est proportionnelle au poids du cycliste auquel on ajoutera le poids du vélo et celui des bagages si vous partez pour une vraie randonnée cyclotouriste. On écrira :

forces de frottement = coefficient de frottement x poids total

Comment déterminer directement le coefficient de frottement ? En théorie, c'est très simple mais en pratique c'est très délicat. On peut concevoir deux méthodes.

Une première méthode consiste à essayer de mesurer directement les forces de frottement. Pour cela, il faut d'abord disposer d'un dynamomètre. On peut en fabriquer un en prenant un élastique de mercerie et en étalonnant son allongement sous l'action de charges différentes. Une fois le dynamomètre réalisé, vous allez sur la chaussée, avec votre vélo et un copain car il faut être deux. Vous choisissez un endroit bien plat, vous enfourchez le vélo et tentez de rester en équilibre en effleurant le sol avec vos pieds ; votre copain vous tracte avec le dynamomètre jusqu'au moment où vous commencez à rouler: à ce moment là, les forces de frottement sont vaincues, vous en déduisez le coefficient de frottement. En fait, c'est assez difficile car les chaussées ne sont pas des plans parfaits, elles sont un peu ondulées, si l'une des roues du vélo se trouve dans un petit creux, c'est raté, votre mesure sera faussée. De plus, vous ne serez pas très sûr que la route est vraiment horizontale, vous devrez faire beaucoup d'essais notamment en positionnant le vélo dans deux directions opposées et faire une moyenne des résultats. Finalement, c'est un peu compliqué et surtout vous risquez de vous énerver et de vous fâcher avec votre copain.

La seconde méthode est peut être plus simple. Un jour sans vent, vous prenez votre vélo et vous allez à l'endroit où une descente s'amorce. Vous enfourchez l'engin sans donner la moindre impulsion, vous décollez les pieds du sol : si vous restez sur place, c'est que la pente n'est pas suffisante pour vaincre la force de frottement, si vous commencez à rouler, c'est que la pente est supérieure au coefficient de frottement. Vous changez de place et, par tâtonnement, vous cherchez l'endroit où vous estimez que vous êtes vraiment à l'équilibre, où un rien vous fait démarrer. On peut démontrer que le coefficient de frottement est égal à cette pente limite, exprimée en %. La difficulté est de mesurer la pente, ce n'est plus un dynamomètre qu'il vous faut, c'est un inclinomètre. On peut en bricoler un assez facilement à partir d'un bon niveau à bulle. On verra plus loin une méthode indirecte pour évaluer le frottement. En pratique, ce coefficient de frottement est de l'ordre de 1%. Cela veut dire qu'avec un vélo de 10 kg et un cyclo de 75 kg, la force de frottement sera de 1% du poids, donc 0,85 kg c'est-à-dire 850 grammes. Avec un revêtement bien lisse, le coefficient sera peut être de 0,75%, avec des gravillons, il pourra atteindre 1,5%.

La force de pesanteur.

Si la route est plate, la force de pesanteur ne vous fait ni avancer ni reculer, elle n'est pas contrariante. Dans une descente, vous l'appréciez car c'est elle qui va vous faire aller de plus en plus vite vers le bas. Cette force n'est pas égale à votre poids mais seulement à une fraction du poids, c'est la composante active qui vous entraîne. Elle est égale à :

force de pesanteur = poids (en Newton) x pente du terrain (en %)

Vérifiez bien vos freins si la pente est forte.

En revanche, dans une montée, cette force, c'est votre cauchemar, c'est comme un boulet à tirer derrière vous, vous regrettez vraiment votre embonpoint.

Nota : pour ceux qui aiment la rigueur mathématique, signalons que si l'on appelle i l'angle de la pente donné par i=Arctg(p), l'équation précédente devrait s'écrire : force de pesanteur= poids x sin(i). Or l'angle i est toujours très faible, tout au moins pour le cyclisme de route. Par exemple, une pente de 10%, pente que l'on ne trouve sur une distance notable que dans certains cols, correspond à un angle de 5.71 degré. C'est pourquoi, la tangente et le sinus de cet angle i peuvent être confondus. Pour p=10%, on a sin(i)=9,95%. Il est impossible dans la pratique de définir une pente avec une précision de 0.05%. De même, en ce qui concerne la loi du frottement, on peut s'affranchir du rôle de la pente en assimilant cos(i) à 1.

La résistance de l'air.

Vous sortez avec une météo superbe, sans vent, mais, dès que vous roulez, ce n'est pas le vent qui se lève mais c'est le vent apparent dû à votre vitesse, celui dont on a déjà parlé. C'est bien pour cela que par forte chaleur estivale vous avez plaisir à rouler, vous sentez du vent, vous suez un peu, l'évaporation vous procure une climatisation naturelle : il ne faut surtout pas s'arrêter. Mais cela a un mauvais coté : plus vous allez vite, plus l'air vous empêche d'avancer, il fait de la résistance. Cette résistance n'est pas proportionnelle à la vitesse, elle est proportionnelle au carré de la vitesse ; si vous allez deux fois plus vite, la résistance devient quatre fois plus importante si bien que plus vous allez vite plus la résistance de l'air vous empêche d'aller vite, à la fin ça devient épuisant, il y a une limite.

Cette résistance s'écrit donc:

résistance de l'air = coefficient x vitesse x vitesse

Le coefficient, on l'appelle Cx, vous connaissez, c'est la même chose pour les voitures. Il dépend de votre position sur le vélo, aérodynamique ou non, de la largeur de votre thorax, de votre taille, de vos vêtements, du profilé de votre casque, etc...

Comment mesurer votre Cx ? C'est très facile. Vous choisissez une grande descente, la plus régulière possible et dont vous connaissez la pente. Vous vous lancez et vous cessez aussitôt de pédaler. La vitesse va croître puis se stabiliser à une certaine valeur. Vous notez la valeur de cette limite. C'est tout. On verra plus loin comment on calcule le Cx à partir de cette expérience.

Dans la région de Fontainebleau, il n'y a pas de descente très longue et il n'est sûr pas que vous ayez atteint votre vitesse limite si vous démarrez gentiment à partir du sommet. Pour y remédier, après un premier essai qui vous donne un ordre de grandeur de cette vitesse, par exemple 40 km/h, vous recommencez le test en prenant de l'élan afin d'arriver à l'amorce de la descente à 40 km/h puis vous cessez de pédaler: votre vitesse va vite se stabiliser, cette fois-ci vous êtes convaincu que vous n'irez pas plus vite.

Nota : pour les puristes en dynamique des fluides, la résistance de l'air est donnée par ½ a Cx S V², S étant la surface frontale de l'objet frappé par le vent, a étant la masse volumique de l'air (de l'ordre de 1,3 kg/m3) et Cx étant le « coefficient de trainée ». Nous avons préféré, pour simplification, intégrer S et a dans le coefficient Cx, ce qui permet de caractériser le cycliste par un seul paramètre, ce paramètre global pouvant être déterminé par l'expérience décrite ci-dessus.

L'équation fondamentale

Si vous voulez avancez, il faudra vaincre toutes ces forces résistantes qui vous contrarient et fournir une force musculaire égale au total des forces résistantes.

Pour évaluer ces forces, désolé, il faut faire un peu de mathématiques. Vous risquez d'être largué mais surtout n'abandonnez pas, on vous attend aux paragraphes suivants, c'est comme au Club où on vous attend toujours en haut des côtes.

Utilisons donc des notations mathématiques ainsi que des unités familières, celles qui s'affichent sur votre balance ou sur le compteur de votre vélo:

f est le coefficient de frottement exprimé en %, par exemple f=1
Cx est le coefficient de résistance à l'air. Il varie de 0.1 à 0.5
W est le poids (cycliste + vélo) exprimé en kilo
p est la pente de la route exprimé en %:
•  positif, la route monte, p= 4 par exemple
•  négatif, la route descend, p= - 4 par exemple
V est la vitesse en km/h

Le total des forces résistantes que nous appellerons Fr est égal à:

forces résistantes = force de pesanteur + force de frottement + résistance de l'air

Avec nos notations mathématiques, cela s'écrit comme suit:

Quant à la force musculaire nécessaire, elle exigera que vous développiez une puissance P. Si vous voulez rouler à la vitesse V, la puissance nécessaire est :

puissance(en watt) = force musculaire (en newton) x vitesse (en m/s)

La force musculaire est donc:

force musculaire= puissance/vitesse

ou encore

L'équation fondamentale s'obtient en écrivant que la force musculaire Fm doit être égale aux forces résistantes Fr.

On aboutit à la relation suivante qui permet de calculer la puissance nécessaire P que vous devez fournir pour avancer à la vitesse V

Nota : pour les puristes, signalons bien que l'accélération de la pesanteur g=9.81 m/s² a été arrondie à 10 m/s².

Le coefficient Cx

Vous avez fait l'expérience peu fatigante décrite ci-dessus consistant à descendre une côte sans pédaler et à noter la vitesse de stabilisation Vs. En fait, dans cette expérience, vous avez développé une puissance nulle, donc P=0

L'équation fondamentale permet alors d'écrire:

Voilà donc comment, connaissant votre vitesse de stabilisation dans une longue descente, vous allez calculer la valeur de votre Cx. Pour vous épargner de sortir une calculette, vous pouvez effectuer le calcul en ligne en cliquant sur ce lien.

Allons sur notre site d'expérimentation favori, la Route Ronde entre le carrefour de Marlotte et Saint Herem. La côte, dans sa partie centrale, est régulière, elle fait 4,4 %, donc p= -4.4.

La vitesse de stabilisation Vs est de 45 km/h. Avec un poids total de 70 kg, donc W=70, un coefficient de frottement de 1, donc f =1, le calcul aboutit à Cx =0,15

Le coefficient de frottement

Nous avons vu précédemment comment on peut essayer de mesurer directement le coefficient de frottement f par deux méthodes. Une troisième méthode tout à fait indirecte mais n'exigeant aucun instrument spécifique, consiste à se lancer sur une route à peu près horizontale, à cesser de pédaler lorsque l'on a atteint une vitesse V₀ et à noter la distance D au bout de laquelle on s'arrête. Cette distance D est liée au coefficient de frottement f par la relation très barbare suivante :

et inversement le coefficient de frottement est lié à la distance d'arrêt D par la relation :

Dans ces formules, nous utilisons des unités de cyclo : V₀ est en km/h, D est exprimé en mètres, f est en %. Ainsi, un cycliste qui pèserait 70 kg avec son vélo, avec un coefficient Cx de 0.20, en roulant à 30 km/h, s'arrêtera au bout de 191 m si le coefficient de frottement est de 1.

Si vous êtes tenté de faire des tests, il vous faut alors encore saisir votre calculette à condition qu'elle soit sophistiquée avec la fonction "logarithme népérien" et il y a des chances que vous fassiez des erreurs mais là encore une bonne surprise vous attend : un calcul en ligne a été concocté afin de vous épargner cette épreuve, il suffit de cliquer sur ce lien.

Et s'il y a du vent ?

Il sera votre allié ou votre adversaire selon qu'il viendra de l'arrière ou de face. Il modifiera la résistance de l'air. Pour le prendre en compte, c'est facile, la résistance de l'air est proportionnelle au carré du vent apparent et le vent apparent est V-Vr si on désigne par Vr la vitesse du vent réel.

L'équation fondamentale devient alors la suivante:

Vr sera positif si le vent vient de l'arrière et négatif s'il vient de face.

Cette relation n'est cependant valable que dans le cas où la vitesse du vent n'est pas supérieure à la vitesse du cycliste. Dans le cas contraire, le vent apparent vient de l'arrière, il agit comme une force motrice et non plus comme une force résistante hostile à votre progression. La relation s'écrit alors :

Mais sur le plat, cela risque de se produire lorsque le vent est très fort. Avec le vent, le Club aime bien rouler à 45 km/h. La vitesse du vent réel devra être encore plus grande. Gare aux zones déventées, aux camions qui vous frôlent, aux branches des arbres qui tombent sur la chaussée dans la forêt de Fontainebleau et pensons aussi au retour. Un marin raisonnable reste au port au-delà de force 7 Beaufort, il est peut-être aussi sage d'en faire autant.

La visualisation de l'équation

Les formules ne sont guère parlantes. Pour les faire parler, on peut faire des applications numériques en faisant varier les données. Pour vous aider, vous pouvez utiliser le petit calculateur proposé ici . On peut aussi se servir de l'équation fondamentale pour tracer des graphiques. Prenons un cyclo dont le poids est de 85 kg, vélo inclus. Il a mesuré son Cx ainsi que le coefficient de frottement. Il a trouvé Cx= 0,20 et f=1

Faisons varier la pente de -12 % à +12 % et traçons les courbes donnant la vitesse du cyclo pour des puissances développées allant de 0 à 500 watts et s'échelonnant de 50 en 50 watts, soit 0, 50, 100, 150,....,500 watts.

On obtient le graphique 1 et on va lui poser des questions.

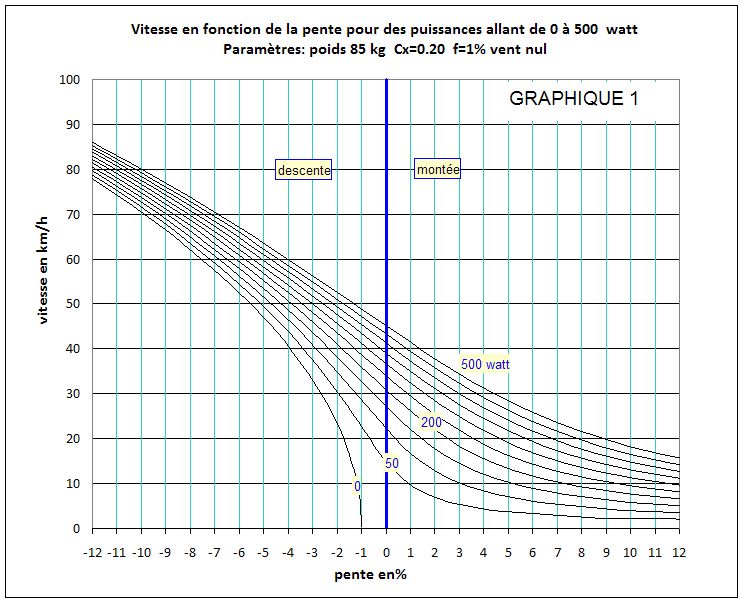
Quelle est la puissance d'un cyclo ?

Il suffit de lire le graphique. Sur le plat, notre cyclo développe 50 watts à 15 km/h, 100 watts à 22,5 km/h, 150 watts à 27 km/h, 200 watts à 31 km/h, 250 watts à 34 km/h. Entre 50 et 250 watts, c'est la puissance fournie par un cyclo. Pour fixer les idées, faisons une comparaison avec un randonneur en montagne: une puissance de 50 watts permet à un randonneur de 75 kg de s'élever de 240 m en une heure: c'est une allure très familiale. Une puissance de 250 watts, c'est grimper 1200 m en une heure: c'est une performance.

Gravir une côte, est ce fatigant ?

En montée, avez-vous vraiment besoin de beaucoup de puissance ? Sûrement pas. Vous pouvez grimper une côte sans aucun effort supplémentaire à condition de réduire considérablement la vitesse. Ainsi si notre cyclo roulait à la vitesse de 22,5 km/h sur le plat, le graphique montre qu'il devra ne pas dépasser 8 km/h dans une côte à 4 %. C'est ce que ne font pas la majorité des cyclistes et c'est bien pour cela que les côtes sont souvent des épouvantails. Retenez donc bien cela: gravir une côte, ce n'est pas fatigant. Vous n'y croyez évidemment pas ? Essayez donc, roulez tranquillement sur le plat puis gravissez une côte à la vitesse mentionnée sur le graphique, vous arriverez en haut tout surpris de ne pas souffler. De plus, si vous disposez d'un cardiomètre, vous constaterez que l'indication n'a pas varié. La difficulté vient peut être du fait qu'il faut un tout petit développement, petit plateau et grand pignon. Ma femme qui gravissait une côte en moulinant beaucoup, peu au fait du jargon cycliste, a très mal interprété la réflexion de deux cyclos  « regarde, elle est aussi grosse derrière que devant ! ». En fait, le problème n'est pas dans les jambes, il est dans la tête. Réduire aussi considérablement la vitesse, ça ne plait pas, c'est comme l'automobiliste qui doit passer de 130 à 90, on n'a pas envie de rouler à la vitesse d'un marcheur, ça serait vexant

Et en montagne ?

La montagne, ce n'est pas autre chose qu'une côte qui n'en finit pas. En adaptant votre vitesse, avec le braquet adéquat, vous n'aurez donc, en principe, pas de difficultés à monter un col. Malgré cela, une crainte vous tenaille : suis-je quand même capable d'arriver au sommet ? C'est là qu'intervient surtout la notion de fatigue. Prenons un col présentant un dénivelé de 1200 m sur 20 km, soit une pente moyenne de 6 %.

Le graphique montre que si notre cyclo a l'habitude de rouler sur le plat à une vitesse moyenne de 22,5 km/h, donc en développant une puissance de 100 watts, il devra gravir le col à une vitesse de 6 km/h pour ne pas affoler le cardiomètre. Il mettra donc 3 heures et 20 minutes pour arriver au sommet. Sur le plat, dans le même temps, à la vitesse de 22,5 km/h, il aurait parcouru 75 km. Voilà donc une méthode pour une estimation prévisionnelle de vos aptitudes de grimpeur: l'équivalence entre l'ascension d'un col et vos parcours habituels sur le plat.

Prenons le Mont Ventoux, 1600 m de dénivelé. La montée au départ de Bédoin fait 22 km donc une pente moyenne de 7.3 % (en fait elle est irrégulière). Le graphique nous indique que, pour notre cyclo qui fournit 100 watts, la vitesse de montée doit être de 5 km/h. Le temps de parcours sera alors de 4 h 24 mn. Sur le plat, cela équivaut à une sortie de 99 km. Si vos sorties habituelles ne dépassent pas 50 ou 60 km, il est certain que l'ascension du Ventoux sera pour vous une performance. Cela ne doit pas décourager: le remède, il suffit de s'arrêter longuement pour que l'ascension puisse être considérée comme deux parcours de 50 km.

Faisons le même calcul pour notre cyclo qui est devenu un « costaud » et qui roule sur le plat à 31 km/h, donc en fournissant une puissance de 200 watts. Il grimpera le Ventoux à 10 km/h sans fournir de puissance supplémentaire. Il mettra donc 2 h 12 mn. Cela équivaut sur le plat à une sortie de 68 km. L'ascension sera donc pour lui une simple formalité.

Pédaler dans les descentes ?

Pour gagner du temps ou rejoindre un groupe, on se dit souvent : je vais rattraper facilement dans la descente qui s'annonce, il suffit que je pédale. Prenons une forte descente, à 6% par exemple; le graphique montre que, sans pédaler, le cyclo atteint 52 km/h. S'il pédale avec vigueur sur un 52/12 en développant 200 watts, il atteindra 59 km/h, ce n'est guère plus. Donc conclusion: ne comptez guère sur les descentes pour rattraper votre retard. Reposez vous en descente, ne pédalez pas, réservez peut être votre énergie pour aller plus loin.

Rouler dans le vent

L'équation fondamentale permet de quantifier l'influence du vent. Le graphique 2 donne la vitesse à laquelle va rouler sur le plat notre cyclo standard en fonction de la vitesse du vent réel et cela pour différentes puissances développées.

Prenons un vent de 20 km/h. Face au vent, notre cyclo roulera à 18 km/h au lieu de 22,5 km/h. Avec le vent dans le dos, il roulera à 27 km/h avec la même puissance.

Lors d'une sortie libre où l'on a le choix d'un parcours, on préfère partir face au vent. Mais attention de ne pas rentrer plus tôt que vous ne le souhaitiez, en faisant demi-tour trop tôt. Vous avez prévu de faire 90 km, 45 km « vent debout » et 45 km « vent arrière », comme disent les marins. Sans vent, la balade serait effectuée en 4 h, donc un demi-tour prévu au bout de 2 h. Si vous ne tenez pas compte de cette météo et si vous faites demi-tour au bout de 2 h, inquiet de voir tourner les aiguilles de la montre, vous aurez parcouru 36 km à l'aller et donc le retour s'effectuera en 1 h 20, votre sortie aura duré 3 h 20 et votre épouse sera surprise de vous voir rentrer à 10 h 50 alors qu'elle vous attendez à 11 h 30.

A quelle heure faut-il faire demi-tour pour rentrer à l'heure prévue ? Une solution serait de vous munir du graphique 2, d'une calculette ou pourquoi pas d'un ordinateur portable. En attendant le jour où votre compteur de vélo, avec un GPS intégré, vous dictera votre conduite, on peut donner une règle pas trop compliquée, exigeant cependant un petit calcul mental qui occupera votre esprit tout en roulant. Tant que le vent réel reste raisonnable, on peut voir sur le graphique que la perte de vitesse vent de face n'est pas trop différente du gain de vitesse vent arrière. Nous vous épargnerons les détails du calcul mais cette constatation permet d'écrire:

Cette relation s'exprime peut être plus clairement comme suit:

Prenons l'exemple précédent. Notre cyclo roule d'habitude à 22,5 km/h. Il part pour une balade de 4 h contre le vent. Il s'aperçoit qu'il roule à 18 km/h. Sa perte de vitesse est donc de 4,5 km/h, ce qui représente exactement 20% par rapport à 22,5. La moitié de la perte de vitesse, c'est donc 10%. Le temps de l'aller sera donc de 50 % + 10 % soit 60 % du temps total. Autrement dit, le temps de l'aller ne sera pas la moitié du temps total mais il faudra ajouter 10 % du temps total, soit 24 minutes. Nous en concluons que la pratique du vélo n'est pas seulement apte à vous maintenir physiquement en forme mais peut également être considérée comme un sport cérébral.

On peut aussi remarquer que la durée totale d'un parcours s'allonge un peu lorsqu'il y a du vent. Avec les mêmes données que précédemment, un parcours de 90 km effectué avec un vent réel de 20 km/h est de 4 h 10 soit 2 h 30 à l'aller et 1 h 40 au retour alors qu'il aurait été de 4 h avec une météo très calme. Vous mettrez donc 10 minutes de plus que le même parcours sans vent, le retour ne vous fait pas gagner suffisamment de temps mais l'écart n'est pas considérable.

Sur le graphique 2, vous remarquerez, pour les courbes correspondant aux puissances de 50 ou 100 watts, ce qui peut vous paraître comme des anomalies avec une allure de méplat. Cela correspond en fait au moment où la vitesse du vent réel devient supérieure à votre vitesse, le vent apparent vient de l'arrière, on peut vraiment dire que le vent vous pousse. Pour une puissance nulle, c'est-à-dire sans pédaler, le graphique vous montre que vous pouvez avancer tout seul dès que le vent devient supérieur à 35 km/h. Avec un vent de 60 km/h (force 7, les véliplanchistes adorent), le cyclo va rouler à presque 30 km/h. Cependant, ces valeurs sont assez approximatives car le Cx n'est pas tout à fait le même si le vent vient de face ou de l'arrière. En toute rigueur, il faudrait le mesurer en reprenant la même expérience de stabilisation de la vitesse dans une longue descente, mais cette fois, il faut descendre en marche arrière. Si vous y arrivez, votre carrière est chez Médrano.

S'abriter du vent.

Il n'est nul besoin de faire des dissertations mathématiques pour vous dire que vous serez bien abrités dans un peloton compact. Lorsque vous roulez, vous heurtez l'air, vous le repoussez sur les cotés, vos créez des turbulences, une surpression devant vous et, derrière, une dépression. Et tous vos copains ou copines souhaitent que vous fassiez une grosse dépression. Personne ne vous soignera, tout le monde veut en profiter.

Le vent apparent est complètement modifié, il diminue fortement si vous vous positionnez astucieusement dans le peloton, vous ne pédalez presque plus. Quelle est la diminution du vent apparent ? Cela devient très complexe, on peut analyser cela en soufflerie ou par des « modèles mathématiques numériques », ce n'est plus notre propos.

Lintérêt pratique serait de répondre à la question suivante: mes capacités sont limitées mais vais-je pouvoir m'intégrer dans un peloton de « costaud », à la condition, bien sûr, de ne pas décrocher ?

Pour y répondre, il suffit de faire quelques expériences simples avec comme seuls instruments votre compteur et votre cardiomètre. Vous étalonnez votre cardiomètre en roulant sur le plat tout seul afin d'établir la relation entre l'indication du cardiomètre et la puissance fournie. Vous voyez qu'en roulant à la vitesse V1, c'est-à-dire avec une puissance P1 que vous déterminez au moyen de votre graphique, la fréquence de vos pulsations est F1. A la vitesse V2, c'est-à-dire avec une puissance P2, la fréquence est de vos pulsations est F2. Cela vous permet d'avoir la relation recherchée entre la fréquence de vos pulsations et la puissance que vous développez.

Maintenant, vous roulez tranquille dans un peloton, vous notez votre fréquence F3 et votre vitesse V3. Cette fréquence est évidemment bien plus basse que la fréquence que vous auriez mesurée en roulant tout seul à la vitesse V3. Vous déterminez  alors:

d'une part la puissance P3 que vous avez effectivement fournie, en vous servant de l'indication F3 du cardiomètre et de votre courbe d'étalonnage
d'autre part la puissance P'3 que vous auriez dû fournir si vous aviez roulé tout seul

La différence P'3 - P3 vous donne le « gain de puissance » qui vous est apportée grâce au peloton, ce gain est évidemment un gain fictif. Vous pourrez alors estimer jusqu'à quelle vitesse vous pourrez vous intégrer dans un peloton.

En fait, tout se passe comme s'il existait un vent réel Vr non nul et qui vous est favorable. En guise de distraction, on peut déterminer la valeur de ce vent fictif au moyen de l'équation fondamentale ou du graphique.

Demandons à notre cyclo standard de faire le test:

il roule tout seul à 22,5 km/h, donc fournit 100 watts. Son cardio est à 120 pulsations
il roule tout seul à 31 km/h, donc fournit 200 watts. Son cardio est à 160 pulsations
il roule maintenant dans un peloton à 35 km/h. Son cardio est à 140 pulsations.

Nous en déduisons que la puissance fournie est alors 150 watts, en admettant qu'elle est proportionnelle à la fréquence des pulsations. L'équation fondamentale ou bien la consultation du graphique 2 permet alors de dire que tout se passe comme s'il existait un vent réel favorable d'environ 15 km/h.

Mais vouloir s'abriter en permanence dans un peloton, c'est vraiment un moyen de se leurrer sur ses capacités réelles. Il faut de plus avoir une grande vigilance pour éviter l'accident et garder en permanence les yeux rivés sur les roues qui vous précèdent. Vous ne voyez plus le splendide paysage qui défile à coté de vous. Ce n'est plus du cyclotourisme.

Le revêtement de la chaussée

Sur un vélo route, nous préférons rouler sur une chaussée bien revêtue. Notre vélo, ce n'est pas un VTT, à chaque vélo son usage. Non seulement un bon revêtement est plus confortable sur nos engins non suspendus, mais il permet d'aller plus vite et donc plus loin pour la même fatigue. A partir de l'équation fondamentale, on a construit le graphique 3 donnant la vitesse sur le plat pour notre cyclo de 75 kg, en fonction de la puissance qu'il développe. Par exemple, pour une puissance de 100 watts, il roulera à 22,5 km/h pour une route standard, passera à 25 km/h sur un billard mais tombera à 20 km/h sur une route gravillonnée. Pour le même effort, il pourra donc faire 10 km en plus ou en moins lors d'une sortie de 4 h.

L'alimentation du moteur

Tout comme votre automobile, la machine humaine a besoin de carburant. Ne vous trompez pas, n'essayez pas de prendre un grand verre de whisky ou de rhum (le rhum, c'est pour les marins qui peuvent se permettre de louvoyer), notre carburant c'est un mélange glucose-oxygène.

L'oxygène, il est dans l'air. Respirez, vos poumons captent l'oxygène de l'air et l'envoient dans le sang. De l'air, vous en aurez toujours assez, même si quelqu'un vous le pompe. Certains pros dilatent leur nez pour éviter les pertes de charge dans la tuyauterie, d'autres facilitent l'absorption de l'oxygène dans le sang par des substances illégales mais là, ne vous trompez pas, nous ne sommes pas des professionnels.

Le glucose, ce sont les aliments qui vous l'apportent. Via la paroi intestinale, il ira lui aussi dans le sang. Le mélange alimentera les cellules musculaires: le moteur tourne. Au départ, du glucose, vous en avez en réserve, il est dans le foie et aussi un peu dans les muscles. Vous avez donc une autonomie. Vos réserves, vous les aurez constituées en absorbant des « sucres lents », par exemple des pâtes ou des féculents, ils contiennent de l'énergie, 1.500.000 joules pour 100 grammes de pâtes. Au bout de quelques heures, si vous ne faites pas le plein, vous risquez la panne sèche. Il vous faut des « sucres rapides », par exemple des barres de céréales, elles contiennent 400.000 joules.

Comme tous les moteurs, le moteur humain n'a pas un rendement de 100%, l'énergie absorbée n'est pas restituée intégralement. En nous basant sur un rendement de 40% (ce chiffre est avancé sans garantie de l'auteur), cela veut dire qu'une barre de céréales pourra vous permettre de fournir seulement 160.000 joules utiles. Notre cyclo de 75 kg roulant à 27 km/h développera une puissance de 150 watts: en une heure, il aura dépensé 3600 x 150 = 540.000 joules; il lui faudra donc au moins trois barres de céréales à l'heure sil ne veut pas puiser dans ses réserves. La sortie va lui coûter cher. Finalement, le vélo, c'est un sport de riches pratiqué par des pauvres.

auteur : fine.jacques@wanadoo.fr
Janvier 2006. Revu en juin 2015

RETOUR ACCUEIL